Algorithm I -- Range-Searchinging in Dictionary for Points

Table of contents:

Quadtrees

• Build Quadtree
• Quadtree Operations
• Quadtree Range Search

kd-Trees

• Construct kd-Tree
• Height kd-Tree
• kd-Tree Operations
• kd-Tree Range Search

Range Trees

• BST Range Search Algorithm
• Range Search Summary
• Range Trees Query Runtime
• Range Search Analysis
• Range Trees Higer Dimensions

Quadtrees

Consider we have n points $S = \{(x_0,y_0), (x_1,y_1), \cdots , (x_{n-1}, y_{n-1}) \}$ in the plane.

Assume: All points are within a square R

• Can find R by computing minimum and maximum x and y values in S
• Ideally the width/height of R is a power of 2

How to build the quadtree on S:

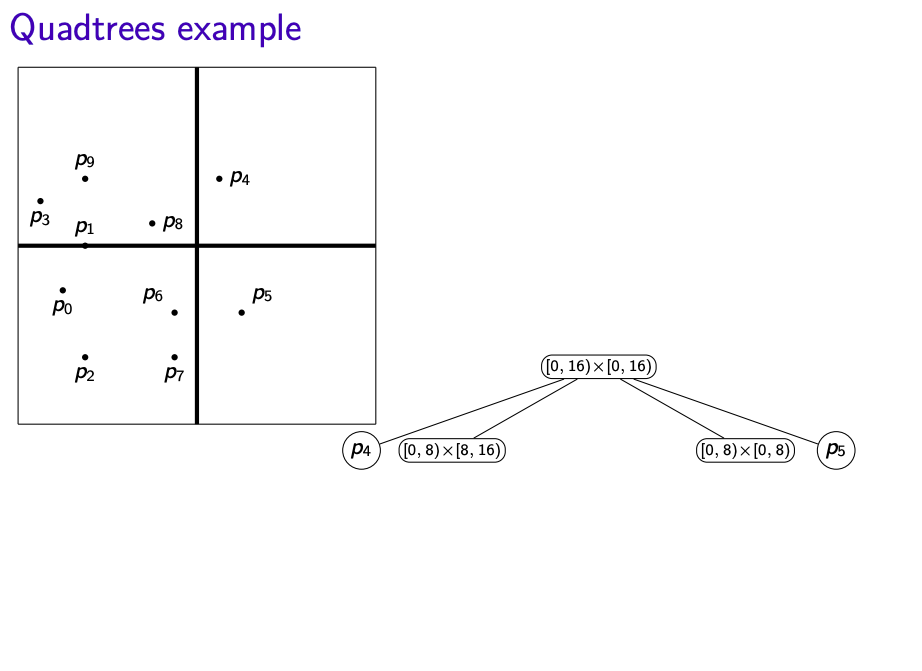
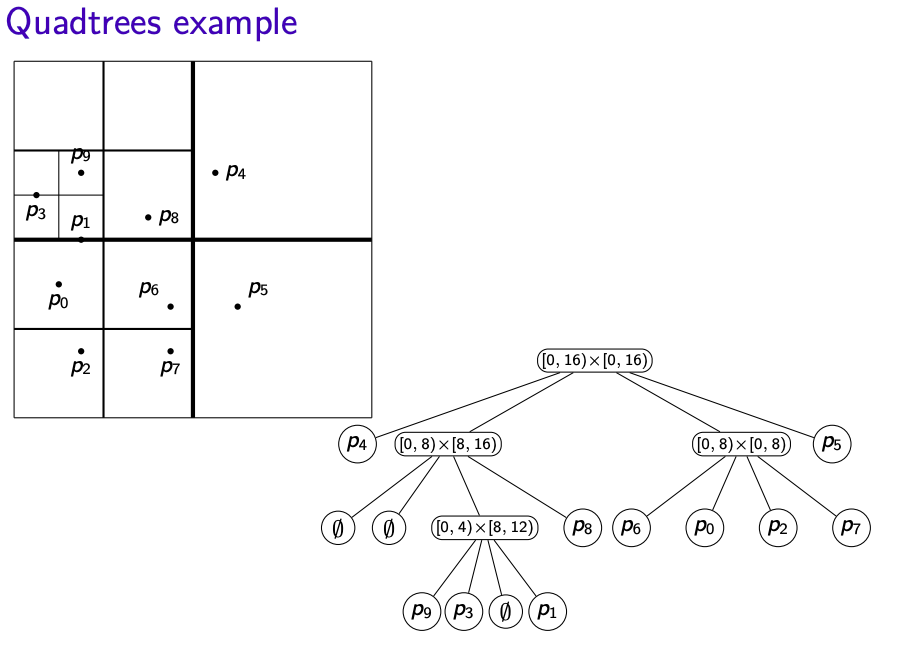
• Root r of the quadtree corresponds to R
• If R contains 0 or 1 points, then root r is a leaf that stores point
• Else split: Partition R into four equal subsquares(quadrants) (i.e. $R_{NE}, R_{NW}, R_{SW}, R_{SE}$)
• Root r then has four subtrees, say $T_{NE}, T_{NW}, T_{SW}, T_{SE}$
• Recursively built the subtree and stop when there is only one point in the square


• Convention: In terms of the points that lie on the split line, we claim that those points belong to right/top side
......

Quadtree Dictionary Operations:

• Search: Similar to binary search trees and tries
• Insert:
  • Search for that point
  • Split the leaf when there are two points in one square.
• Delete:
  • Search for the point
  • Remove the point
  • If its parents has only one point left, then delete the parents (recursively to all its ancestors that have only one point left)

Quadtree Range Search

• Alogrithm:
QTree-RangeSearch(T,A)
1. T: The root of a quadtree, A: Query rectangle
2. $\quad$ let R be the square associated with T
3. $\quad$ if $R\subset A)$ then
4. $\qquad$ report all points in T; return
5. $\quad$ if $(R \cap A\,\,is\,\,empty)$ then
6. $\qquad$ if p is in A return p
7. $\qquad$ else return
8. $\quad$ for each child vi of T do
9. $\qquad$ QTree-RangeSearch(v,A)

• Time analysis:
  • Might have bad distribution of points
  • spread factor of points $S: \beta(S) = \frac{sidelength\,\,of\,\,R} {d_{min}}$
  • where $d_{min}$ is the minimum distance between two points in S
  • height of the quadtree: $h\in \Theta (log \beta(S))$
  • Complexity to build initial tree: $\Theta(nh)$ worst-case
  • Complexity of range search: $\Theta(nh)$ worst-case even we found nothing

kd-trees

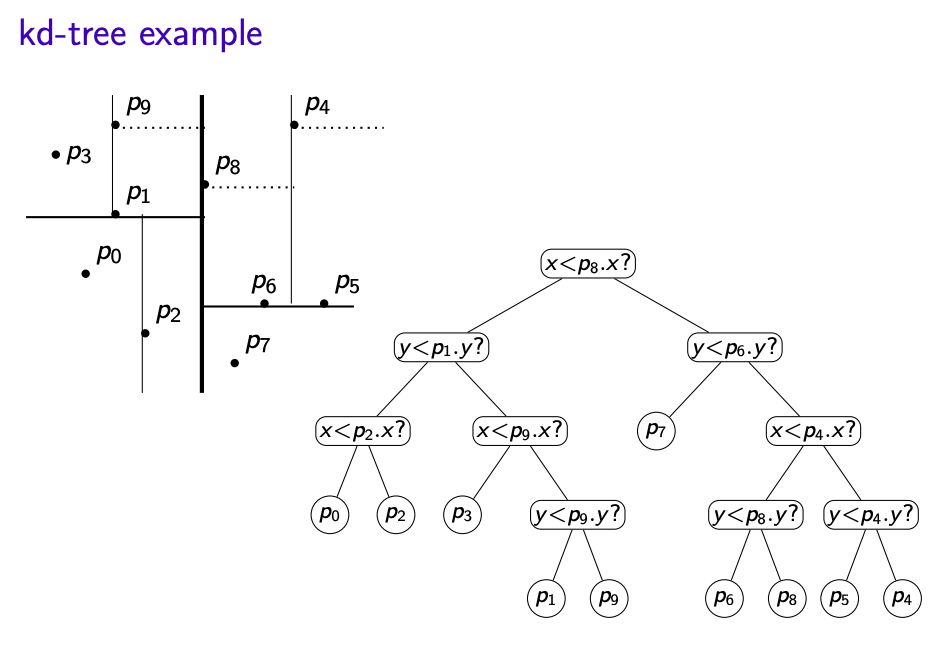
• Suppose we have n points $S = \{(x_0,y_0), (x_1, y_1), \cdots, (x_{n-1}, y_{n-1})\}$
• Split the region such that roughly half the point are in each subtree
• Each node of the kd-tree keeps track of a splitting line in one dimension (either vertical or horizontal)
• Convention: Points on split lines belong to right/top side
• Keep splitting, switching between vertical and horizontal lines, until every point is in a separate region

Constructing kd-trees

Build kd-tree with initial split by x on points S:

• If $|S| \le 1$ create a leaf and return
• Else X:= Quick-Search(S,$\lfloor\frac {n} {2} \rfloor$ (select by x-coordinate)
• Partition S by x-coordinate into $S_{x<X}$ and $S_{x\ge X}$
• Create left subtree recursively (splitting by y) for points $S_{x<X}$
• Create left subtree recursively (splitting by y) for points $S_{x\ge X}$
......

Analysis

• Find X and partition S in $\Theta(n)$ expected time
• $\Theta (n)$ expected time on each level in the tree
• Total is $\Theta(height \dot n)$ expected time
• Be able to reduced to $\Theta(nlogn + height \dot n)$ worst-case by pre-sorting (will be explain in the future)

kd-tree height

Assume first that the points are in general position(no two points have the same x/y-coordinate)

• $\lfloor \frac{n} {2} \rfloor$ points have been evenly puts into two sides
• height h(n) satisfies the recursion $h(n) \le h(\lceil \frac {n} {2} \rceil) + 1 $; this gives us $h(n) \le \lceil log(n) \rceil$
• thus we can build the kd-tree in $\Theta(nlogn)$ time and $O(n)$ space

kd-tree Dictionary Operations

• Search: similar to binary search tree by suing indicated cooridinate
• Insert: search, insert as new leaf
• Delete: search, remove leaf and unary parents

After insert or delete, the split might no longer be at exact median and the height is no longer guaranteed to be $O(logn)$ even for points in general position.

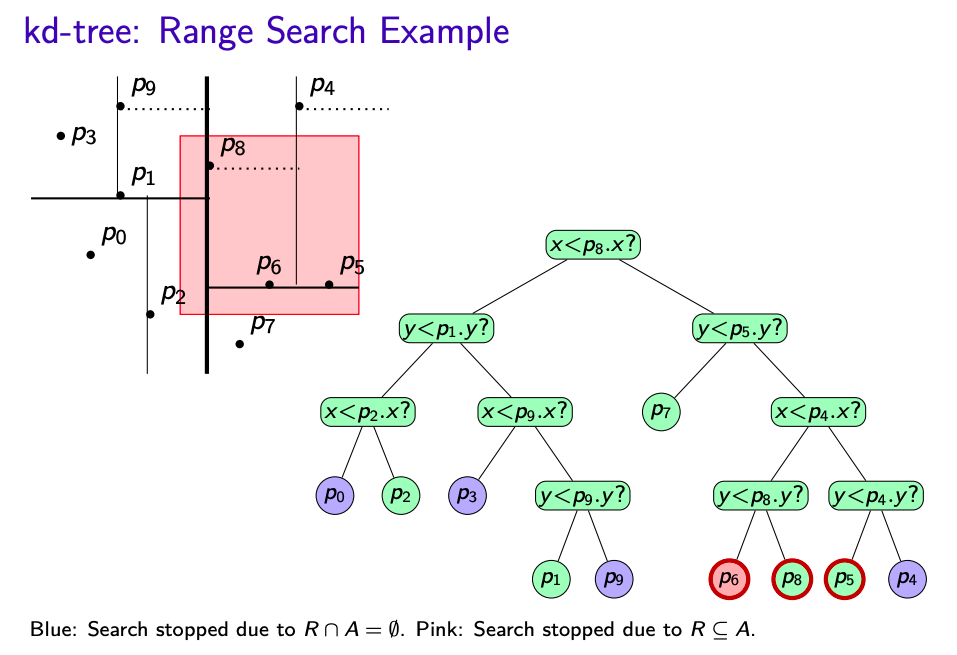
kd-tree Range Search

• every node is associated with a region

kd-Tree RangeSearch(T,R,A) T: The root of a kd-tree, R: region associated with T, A: query rectangle
1. $\quad$ if ($R\subset A$) then report all points in T; return
2. $\quad$ if ($R\cap A$ is empty) then return
3. $\quad$ if (T sotres a single point p) then
4. $\qquad$ if p is in A return p
5. $\qquad$ else return
6. $\quad$ if T stores split "is x < X"
7. $\qquad R_{l} = R \cup \{(x,y) : x < X\}$
8. $\qquad R_{r} = R \cup \{(x,y) : x \ge X\}$
9. $\qquad$ kdTree-RangeSearch(T.left, $R_l$, A)
10. $\qquad$ kdTree-RangeSearch(T.right, $R_r$, A)
11. $\quad$ else
12. $\qquad R_{l} = R \cup \{(x,y) : y < Y\}$
13. $\qquad R_{r} = R \cup \{(x,y) : y \ge Y\}$
14. $\qquad$ kdTree-RangeSearch(T.left, $R_l$, A)
15. $\qquad$ kdTree-RangeSearch(T.right, $R_r$, A)

kd-Tree Range Search Complexity

• The complexity of range search in kd-trees is $O(s + \sqrt {n})$, where s is the number of reported points
• s can be anthing from 0 to n
• No range-search can work in o(s) time since it must report the points
• Q(n) is the number of "green" nodes:
  • kdTree-RangeSearch was called
  • Neither $R\in A$ nor $R\cap A = \emptyset$
• Q(n) satisfies the following recurrence relation: $$Q(n) \le 2Q(n/4) + O(1)$$
• This solves to $Q(n) \in O (\sqrt{n})$
• For the higher dimensions:
  • we have storage: $O(n)$
  • Construction time is: $O(nlogn)$
  • Range query time: $O(s+n^{1 - 1/d})$

Range Trees

• Apply time-space trade off, might waste in space but faster in search.
• Have a binary search tree T (sorted by x-coordinate); --> primary structrue
• Each node v of T has an auxiliary structure T(v): a binary search tree (sorted by y-coordinate)

BST Range Search

BST-RangeSearch(T, $k_1$, $k_2$)

T: root of a binary search tree, $k_1$, $k_2$: search keys
Return keys in T that are in range[$k_1,k_2$]
1. $\quad$ if T = null then return
2. $\quad$ if $k_1 \le key(T) \le k_2$ then
3. $\qquad$ L = BST-RangeSearch(T.left, $k_1,k_2$)
4. $\qquad$ R = BST-RangeSearch(T.right, $k_1,k_2$)
5. $\qquad$ return $L\cup \{key(T)\} \cup R$
6. $\quad$ if key(T) < $k_1$ then
7. $\qquad$ return BST-RangeSearch(T.right, $k_1,k_2$)
8. $\quad$ if key(T) > $k_2$ then
9. $\qquad$ return BST-RangeSearch(T.left, $k_1,k_2$)

Note: Keys are reported in in-order, i.e. in sorted order.

Range Search Summary

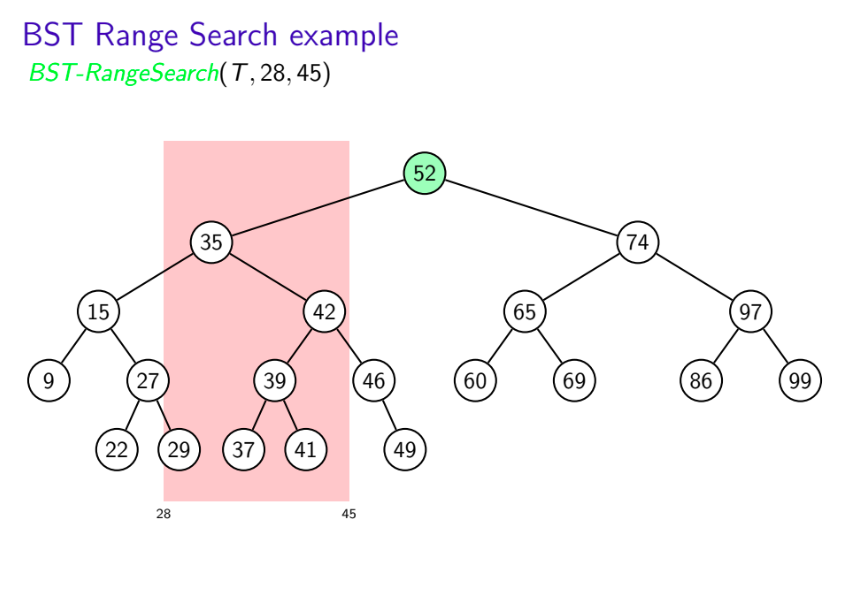
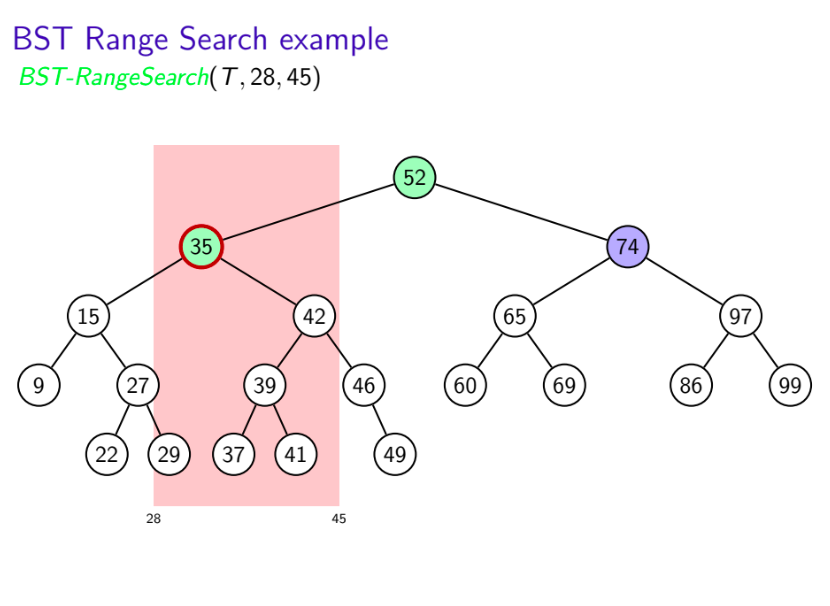
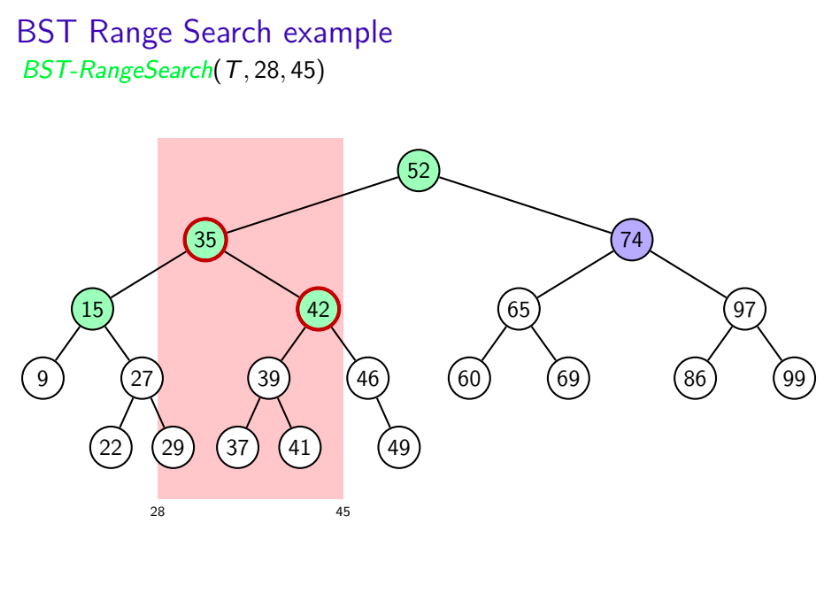
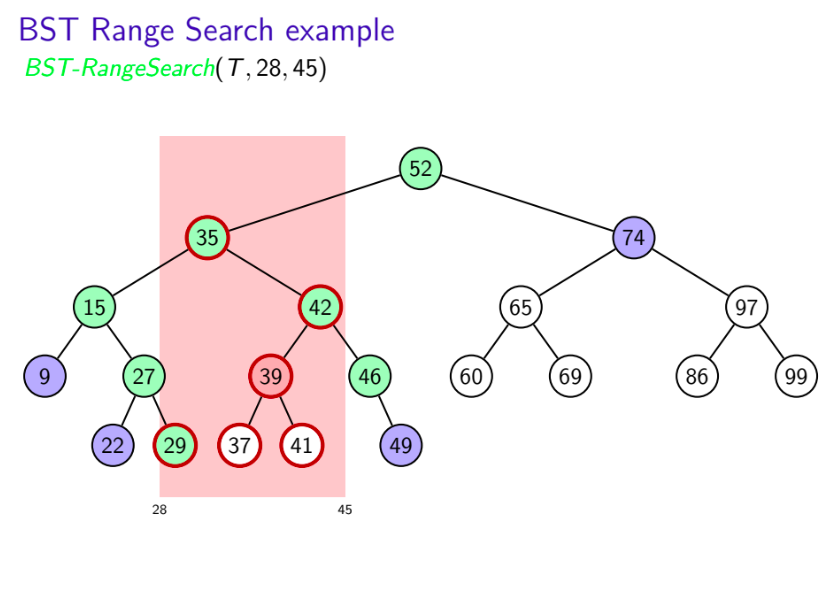
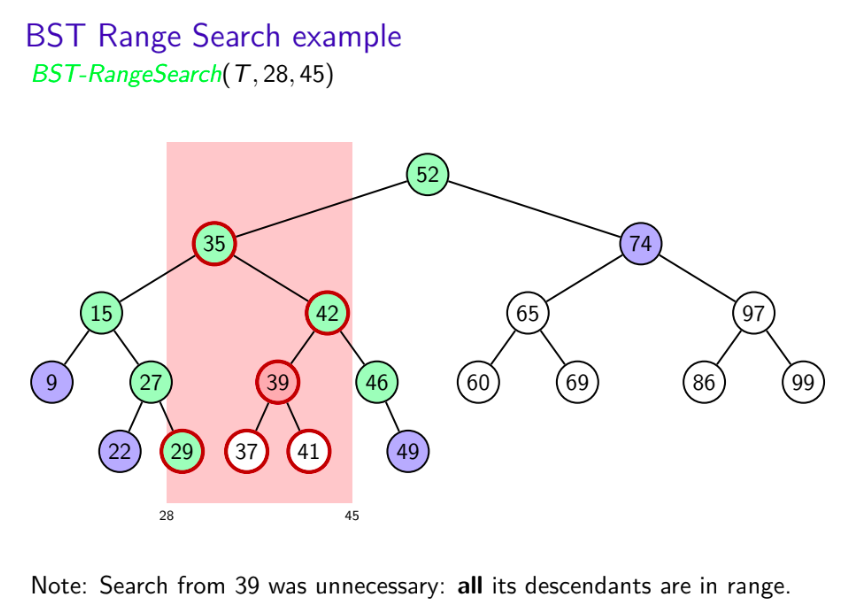
• Search for left boundary $k_1$ gives path ${\color{green} {P_1}}$
• Search for right boundary $k_2$ gives path ${\color{green} {P_2}}$
• Partition nodes of T into three groups:
  • ${\color{green} {boundary\,\,nodes:}}$ nodes in $P_1$ or $P_2$
  • ${\color{red} {inside\,\,nodes:}}$ nodes that are right of $P_1$ and left of $P_2$
  • ${\color{blue} {outside\,\,nodes:}}$ nodes that are left of $P_1$ or right of $P_2$
• Report all inside nodes
• Test each boundary node and report if if it is in range

Range Search Analysis

• Search for path ${\color{green} {P_1}}$: $O(logn)$
• Search for path ${\color{green} {P_2}}$: $O(logn)$
• $O(logn)$ ${\color{green} {boundary\,\,nodes}}$
• There are many inside nodes.
• We only need to topmost of them: allocate node v
  • not in $P_1$ or $P_2$, but parent is in $P_1$ or $P_2$ (but not both)
  • if parent is in $P_1$, then v is right child
  • if parent is in $P_2$, then v is left child
• O(logn) allocation nodes. For each of them report all descendants
• Similar to before, test each boundary node and report it if it is in range

• Run-time: O(#boundary nodes + # reported points) = O(logn + s)

Range Trees: Query Run-time

• O(logn) time to find boundary and allocation nodes in primary tree
• There are O(logn) allocation nodes
• O(logn + s) time for each allocation node v
• Two allocation nodes have no common point in their trees, so $\sum s_v \le s$
• Time for range-query in range tree: ${\color{red} {O(s+log^{2}n)}}$

Range Trees: Higher Dimensions

• Range trees can be generalized to d-dimensional space.
  • Space: $O(n(logn)^{d-1})$
  • Construction time: $O(n(logn)^{d-1})$
  • Range query time: $O(s+(logn)^d)$